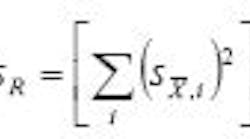Last time (CP, October, p. 57), Dr. Gooddata discussed the five types of systematic error (bias) and commented on how important it was to estimate their potential magnitudes or systematic uncertainties (bias).

Note the ambiguity of the term “bias.” Many people use it to refer to the systematic error for a single measurement. They say “bias” to mean the actual difference between their measurement and the true value of the test. In contrast, others at times will estimate the potential magnitude of this type of error and call that the “bias.” Here they mean the +/- interval about the measurement that estimates the possible extent of the true systematic error.

Confused? So am I. Dr. Gooddata, therefore, recommends that we largely abandon the term “bias.” Instead, we will use the terms “systematic error” and “systematic uncertainty.” Systematic error is the actual error that exists between a measurement and the true value with zero random errors. Systematic uncertainty is taken to mean the estimate of the systematic error’s limits that we could expect with some confidence.

Collective wisdom

The International Standards Organization’s (ISO) “Guide to the Expression of Uncertainty in Measurement” recommends that uncertainty analysts (that’s you) assign both a distribution and a confidence interval to each systematic uncertainty estimated. The U.S. National Standard on test uncertainty, “ASME PTC19.1 — Test Uncertainty,” has been rewritten and recommends that estimates of systematic uncertainties be assumed to represent a Gaussian-Normal distribution and be estimated at 68% confidence. (That would make systematic uncertainties’ estimates of one s_x, as the degrees of freedom are assumed to be infinite for each of these systematic uncertainties.)

Remember, too, that the combined effect of several sources of systematic uncertainty is still determined by the root-sum-square method. The result is the interval that contains the true value 68% of the time in the absence of random errors (whose limits we now estimate with “random uncertainties.”)
The systematic uncertainty of the result would then be:

 

where each b_i is a 68% confidence estimate of the systematic uncertainty for source i. This allows us to work with equivalent s_x values throughout this analysis. We will need that capability when we also deal with the random uncertainties.

As for those random uncertainties, the latest U. S. National Standard recommends (as does the ISO Guide) estimating their magnitude limits as one standard deviation for the average at a particular level in the measurement hierarchy. That is, the random uncertainty for an uncertainty source is the standard deviation of the average for that uncertainty source. It is noted as one s_x. Here too, the random uncertainty for the test result is the root-sum-square of the random uncertainties for each level in the measurement hierarchy.

The random uncertainty of the result is then:

where each _x,i is the standard deviation of the average for that level in the measurement hierarchy.

Note that with this approach we are working with equivalent s_x values for both systematic and random uncertainties. Why is this important? How does this help us? Let’s see.

A singular task

Now that we are all experts in the determination of the systematic and random uncertainties of a measurement, the question we must approach with exceptional anticipation is this: “What good is it to calculate only systematic and random uncertainties? Shouldn’t we find a way to combine them into an overall uncertainty for the measurement result?” (I know that’s two questions.)

For a long time there were two primary approaches to this problem of calculating a single number to represent the measurement result uncertainty. Those two uncertainty models (kind of like Ford and Chevy for car buffs) were the U_ADD and the U_RSS models. These were also known as U₉₉ and U₉₅, respectively, because the former provided approximately 99% coverage and the latter approximately 95%.

Well, what were these models and isn’t there something better after all these years?

The U_ADD model was:

The U_RSSmodel was:

 

Note that when it is said that <ital>U<subscript>ADD<end subscript, end ital> provides approximately 99% coverage (not confidence) and<ital>U<subscript>RSS<end subscript, end ital> approximately 95%, the key words are approximately and coverage.
We use approximately because these coverages were determined by simulation, not statistics. They are right in the long run, but not exact. Why do we use the term coverage and not confidence? What is this coverage thing? Why not express these uncertainty intervals (hint, new word there) as confidence intervals? The reasoning is: The systematic uncertainty, <ital>B<subscript>R<end subscript, end ital>, was an estimate of the limits of systematic error to about 95% coverage. <ital>B<subscript>R<end subscript, end ital> was not a statistic but an estimate. <graphic>  is, however, a true statistic. It is appropriate to speak of confidence only with a true statistic.
Both of the above uncertainty equations combine a statistic, <graphic> , with a non-statistic, <ital>B<subscript>R<end subscript, end ital>. The result cannot be an interval (that new word) with a true confidence but rather provides coverage as documented by simulation.