Achieving more efficient operation often means adjusting several variables that might conflict with each other, e.g., better quality sometimes mandates a lower production rate and higher energy consumption. So, determining the best operating conditions requires knowledge of the quantitative effects of several variables on parameters of interest. These relations tend to be complicated. Physical models usually don't describe industrial production processes accurately enough. On the other hand, empirical and semi-empirical modeling approaches don't demand any significant assumptions or simplifications.
Conventional empirical modeling relies on linear statistical techniques that have severe limitations. In contrast, new nonlinear modeling techniques can derive knowledge about complicated nonlinear effects of variables from production data, taking nonlinearities into account. Such nonlinear models of a tall oil distillation column implemented at Forchem Oy in Finland have helped improve the operation of the process.
Tall or pine oil is a byproduct of pulping of pine wood via the Kraft process. Tall oil contains mostly acidic but also some neutral components. Forchem uses a series of distillation columns to separate it into rosin, fatty acids, heavy oils and pitch. Rosin consists mainly of rosin acids, particularly abietic and pimaric acids, which also are referred to as resin acids. For rosin production, water and turpentine are first removed from the raw tall oil received from a pulp mill. The tall oil then passes to a distillation column that produces raw fatty acids as the overhead stream and a bottoms containing mostly rosin. A portion of this heavy fraction goes to the pitch column. Rosin is taken out somewhat above the bottom. This distillation is energy intensive and significantly affects profitability of production.
The acid value of tall oil is typically around 140 while the rosin acid content is about 30% for Forchem's raw material. Rosin distilled from this oil typically contains 90% rosin acids and has a softening point of around 60°C–65°C.
WHY NONLINEAR MODELING?
Better quantitative knowledge of the effects of process variables and feed characteristics can enable efficiency improvements. However, these relationships tend to be complicated for distillation processes, like many industrial operations. Physical modeling only provides modest accuracies in predicting most of the interesting consequences of distillation like product purity and energy consumption — partly because it requires plenty of assumptions and simplifications, and partly because sufficient knowledge of the thermodynamics of each component in tall oil is lacking. In constrast, empirical and semi-empirical modeling suffers neither of these limitations. It just needs an adequate amount of production data with a fair variation in the variables of interest.
Simpler nonlinear modeling approaches include polynomial regression and linear regression with nonlinear terms. Nonlinear regression is useful in some situations. However, these older techniques require specifying the form of the nonlinearities. Newer techniques, including series of basis functions, splines, kernel regression, and feed-forward neural networks, are based on free-form nonlinearities.
To try to improve the tall oil distillation process, we chose an empirical approach based on feed-forward neural networks. Such networks are a set of efficient tools for nonlinear modeling, particularly because of their universal approximation capability [1]. They can be applied to individual unit operations or entire trains, whether batch or continuous, and regardless of the type of chemical or other process [2].
The process models are developed from data on feed characteristics, process variables, as well as properties and flow rates of outgoing streams, to determine the best values of process variables to maintain operation within desired limits while also satisfying economic criteria (such as maximum yield, purity, production rate or energy efficiency, and minimum raw material consumption or defects). Many books, including Ref. 3, describe various techniques for this kind of optimization problem.
DEVELOPING THE MODELS
We identified a number of variables to use for developing the nonlinear models, and had production data from January 2009 onwards. Production data tend to be dilute in information and often contain misleading observations. So, we carefully selected data, excluding some observations from the model development set. Doing so enabled us to make more progress in a shorter time period — the model development project started in February 2011 and finished in June. Figure 1 shows the kinds of variables included in the models. Testing indicated the models were good quality.
Figure 2 compares the measured values of energy consumption of the distillation with values predicted by the nonlinear model. These nonlinear models then were implemented in a LUMET system, a set of software components meant to make use of the models easy for people not familiar with nonlinear modeling.
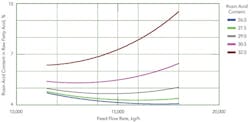
The models allow us to see the individual and combined effects of the input variables on the outputs. Figure 3 shows the interesting cross-effect of feed flow rate and rosin acid content in raw fatty acids. At lower rosin contents, higher feed flow rates are preferable for a given production rate. However, for higher rosin contents, lower feed flow rates lead to smaller losses of rosin acids through the fatty acid stream. For the typical case of a medium amount of rosin in the feed, there is an optimum feed flow rate that minimizes loss of rosin acids in the raw fatty acid stream. Ideally, of course, we strive to maximize rosin and raw fatty acid flow rates while trying to get as much of the rosin acids as possible in the rosin and minimizing the rosin acids in the raw fatty acid stream. Some input variables have desirable effects on some outputs but undesirable effects on others. These and other such conflicting objectives make it a challenging task to determine the best ways of operating the column.
THE BENEFITS
Mathematical models can contain a lot of valuable quantitative knowledge in a concise and a precise manner. However, concrete benefits only result if the models are used efficiently. LUMET systems, which have been developed over 15 years, offer several features that make it easier to utilize the model for several kinds of calculations.
One shift supervisor, the fourth author of this article, expects the models to help both experienced as well as inexperienced operators operate the column better — particularly when dealing with uncommon situations. The production director, the second author, believes operators' use of the models should lead to higher yields and lower energy consumption while ensuring quality in terms of softening point and rosin acid content of the rosin.
The nonlinear models have helped improve the operation of the distillation column right from the first day. Seven and a half hours after the LUMET system went into use, rosin yield was increased by more than 8%, energy consumption was lowered by about 6%, and the rosin acid loss through the raw fatty acid stream was reduced by around 0.3%. This very good improvement can't be expected every time. However, over the following days, a rosin yield increase of about 3% usually was possible with little effort and without much change in energy consumption. Increased production from a boost in yield of only 1.5% conservatively is worth more than €500,000 ($700,000) per year. The use of the models essentially has raised rosin production capacity as well as operating efficiency.
CONSIDER NONLINEAR MODELS
Plants usually collect a lot of production data that go unused or under-utilized. Nonlinear modeling provides a way to extract valuable information from those data — and thus for plants to get more out of their equipment and raw materials while also improving control over product properties. If used effectively, it can add to a company's competitiveness.
ABHAY BULSARI is technical manager for Nonlinear Solutions Oy, Turku, Finland. TIMO SAARENKO is production director, JAANA VALTANEN is a quality assurance engineer, and LAURA KASKINEN is a shift supervisor for Forchem Oy, Rauma, Finland. E-mail them at [email protected], [email protected], [email protected] and [email protected].
References
1. Hornik, K., Stinchcombe, M. and White, H., "Multilayer Feedforward Networks Are Universal Approximators," Neural Networks, Vol. 2, p. 359 (1989).
2. "Neural Networks for Chemical Engineers," A. Bulsari, ed., Elsevier, Amsterdam (1995).
3. Gill, P. E., Murray, W. and Wright, M. H., "Practical Optimisation," p. 136, Academic Press, London (1981).