1660320764523 Figure 1 Flowresist Standard Resized

View Data from a Different Perspective

July 23, 2009

Re-plotting by flipping the parametric lines can provide important insights.

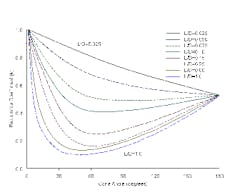
Flow can go into a pipe from a large tank via a variety of entrance shapes. We already have looked at the resistance coefficients of some of the more common ones (http://www.ChemicalProcessing.com/articles/2009/107.html). This month we cover a conical nozzle projecting into the tank — and use its data to make some more general points. [pullquote] Figure 1 gives the standard presentation of resistance coefficient, k, versus cone angle with parametric lines of L/D. L is the length of the conical section of pipe that extends into the tank and D is the diameter of the pipe. The figure by itself is unexceptional. However, let’s re-plot the data with k and L/D as axes with parametric lines for angles (Figure 2). To reduce confusion, the plot only shows lines for cone angles of 10° to 90°. Points on each line indicate the tie points used to convert Figure 1 to Figure 2 (with smaller points used in the crowded region of 50° to 90° to prevent cluttering the graph).

Standard Presentation

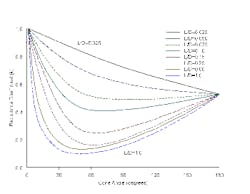
Figure 1. Flow resistance coefficient usually is plotted against cone angle. Figure 2 has an anomaly that should give pause and points up a second, important factor in fluid flow much more clearly than the conventional presentation. The 10° angle line has an inflection point at an 0.15 L/D ratio. I’ve learned from unfortunate experience to worry about inflection points in graphs. Unless you absolutely trust the data, take extreme care. In this case, the consequences likely are small — but the appearance of the inflection point illustrates the value of flipping parametric lines on graphs. It’s a powerful technique to check data consistency. If graphs behave when switching parameters, they’re much more likely to be giving realistic results.

Different Perspective

Figure 2. Switching parameters for the axes reveals an inflection point. Second, Figure 2 shows that 60° provides close to the minimum k for any L/D ratio. The resistance coefficient represents energy loss — the lower the energy loss, the lower the k. In the absence of other factors (such as obstructions, vanes, fans, etc.), flow systems operate at the lowest energy-loss level possible. This leads to a final point: systems that use an obstruction to smooth out flow but have a recovery angle significantly deviating from about 60° will suffer some degree of maldistribution. Whenever you see systems with large changes in flow path, always ask what drives the flow, why should flow patterns be smooth, and how flow really may act? Over the years, the 60° rule has proven useful in troubleshooting combustion systems, large heat exchangers, air-fin exchangers, air ducting, reactors, fired heaters, vessel internals and many other units. Applying basic rules of thumb isn’t always the entire or final answer, but it’s an efficient place to start. Andrew Sloley is a contributing editor to Chemical Processing. You can e-mail him at[email protected]