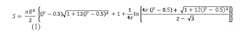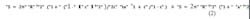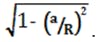Find Tank Wetted Surface Area

where F is fractional fill height, h/2R, where h is the height of fluid in the head, R is the radius of the tank (and head), and ε is the eccentricity of the ellipse defining the tank head by rotation around its minor axis. Even though Eq. 1 is a function of ε, it only can be valid for ε = √3/2 (i.e., a 2:1 ellipsoidal head); this can be shown simply by doubling the surface area for a half-full tank (F = 0.5) and equating that to the surface area for a full tank (F = 1). Solving that equation for ε yields a unique value of ε = √3/2. Eq. 1 also gives the correct wetted surface areas for half-full and full heads as can be shown using well-known surface areas for oblate spheroids [2]:

where the eccentricity has been eliminated to provide a practical equation for tank heads in terms of a — the protrusion of the tank head beyond the end of the cylindrical portion of the tank, i.e., ε =

Even though Eq. 1 is correct for the 2:1 head at half-full and full values, it is not rigorous for other fill levels, including the wetted surface area for h = 0, which must be 0 for heads of all ε (i.e., a). If a fill level of 0 is put in Eq. (1), the surface area, S, is found to be a function of ε, i.e., S = (πR2⁄8ε) ln[(2 – 2ε)⁄(2 – √3)]. So for an empty tank, Eq. 1 can’t be valid unless ε = √3/2.

Broader Suitability

A rigorous equation valid for the wetted surface area for any hemispheroidal head (one head only) of any diameter, fill height and a (and, hence, ε) is:

This equation simplifies for some special cases of hemispheroidal heads:

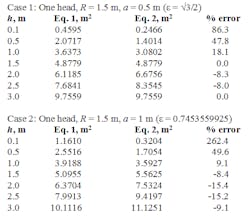
Table 1 compares the wetted surface areas of hemispheroidal heads at various fill heights calculated using Eq. 1 to rigorous values calculated using Eq. 3 for a head of radius 1.5 m for two different values of a (i.e., ε) and shows the percentage error in values calculated with Eq. 1.

Using Eq. 1 can result in quite a large error in a wetted surface area calculation for a hemispheroidal head — but the total error over the entire tank may be inconsequential, especially because large safety factors usually are applied to theoretical calculated values. However, there is no good reason to use approximate calculations given the available rigorous equations, which many graphing calculators can easily and rapidly solve.

Figure 1. Ref. 1 used this cylindrical vessel with 2:1 hemispheroidal heads for an example calculation.

Let’s compare the results for the wetted tank area example given in Ref. 1 with the area found using rigorous Eq. 3. As shown in Figure 1, the example tank has a horizontal cylindrical body 6 m long and a diameter of 3 m. The heads are 2:1 hemispheroidal heads, i.e., a = 0.75 m. The fluid level is 1 m. Using Eq. 1, the wetted area of both heads is 7.2746 m². Standard well-known formulas for calculating the wetted surface area of the cylindrical portion of the tank give 22.1573 m². So, the total tank wetted surface area is 29.4319 m². In contrast, using Eq. 3, the correct area for both heads is 6.1604 m² — adding the cylindrical area gives the correct total tank wetted surface area of 28.3177 m². Thus, the error in total tank wetted surface area is 3.9%, although the wetted head surface area is in error by 18.1%.

An additional bonus of using Eq. 3 is that it handles all values of a — i.e., it is valid for flat heads (a = 0), hemispherical heads (a = R), oblate hemispheroidal heads (a < R) and prolate hemispheroidal heads (a > R).

Equations for wetted surface areas of horizontal and vertical cylindrical tanks with conical, guppy and torispherical heads are available as are equations for horizontal elliptical tanks with hemiellipsoidal heads [3].

DANIEL E. JONES, PhD, PE, is a Grapevine, Texas-based consultant. Email him at [email protected].

REFERENCES
1. Doane, Richard C., “Accurate Wetted Areas for Partially Filled Vessels: Accurately Determine Wetted Surface Areas Needed for Fire Relief Applications,” p. 56, Chem. Eng’g, Dec. 2007.
2. Weisstein, Eric W., “CRC Concise Encyclopedia of Mathematics,” 2nd edition, p. 2,052, Chapman & Hall/CRC, Boca Raton, Fla. (2003).
3. Jones, Dan, “Calculating Tank Wetted Area."