Jacketed Reactor
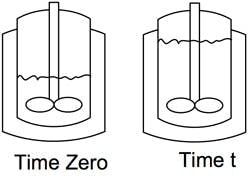
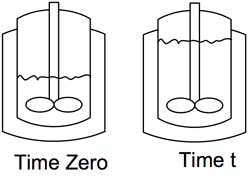
Figure 1. Equation assumes that batch always is on the straight wall of vessel.
For simplification, let’s assume the liquid mixture in the reactor prior to addition is on the straight wall as shown in Figure 1. For purposes of integration, let’s also assume the heat of reaction (ΔH), liquid density (ρ), overall heat transfer coefficient (U) and temperature differential (ΔT) between the utility (jacket) and process (tank) remain constant.
This situation is the reverse of a batch distillation — for which the equations and their derivation have been published previously [1]. The solution is:
At/A0 = e–t/Θ (1)
where Θ = ρ×D×ΔH/(4U×ΔT) (2)
The differences versus batch distillation are in the definition of the terms ρ, ΔH and ΔT. Let’s discuss each of these.
Liquid density. In batch distillation, ρ is the density of the liquid in the vessel. For reagent addition, this term is the net weight added during the addition versus the observed volume change of the reaction mix. For the special case where the reagent and reaction mixture mix ideally with a zero volume change, the density equals that of the reagent.
Enthalpy change. In batch distillation, ΔH is the heat of vaporization of the evaporated solvent. For reagent addition, it is the heat of reaction expressed as unit of heat versus the net weight added. The heat of reaction must be calculated at the temperature of reaction and must include all enthalpy effects such as the sensible heat from a reagent below reaction temperature, heat of dilution, evaporative cooling when there is a byproduct off-gas and, of course, the chemical heat of reaction.
Temperature difference. The ΔT term is the same and constant for both batch distillation and reagent addition. Typically in batch distillation, steam is the heating medium and calculation of this term is straightforward because both the process and jacket are isothermal. In reagent addition, a liquid commonly is the coolant and the jacket supply and outlet temperature are unequal. In this case, the difference is determined by a log mean temperature calculation.
For a simple case of water flowing once through a jacket, the following relationships apply:
TO = TP + (TS - TP)/K (3)
where K = exp [(UA)/(WCp)] (4)
Eq. 4 includes the wetted area (A). Under a rigorous analysis, the temperature difference is not constant. However, as an approximation, the log mean temperature difference can be calculated at both the lowest level (A0) and highest level (At) in the integration. For practical problems, the observed disparity in temperature difference will be slight and the lower value can be used to provide a conservative estimate of addition time. An example will illustrate this.
Many reactors have heat/cool modules that enable the jacket inlet temperature to differ from the coolant supply temperature. In such cases, substitute equations that are available in Reference 2 for Eq. 3 and Eq. 4.
An Example
Molten sodium metal is added to water to make a sodium hydroxide solution — with the temperature controlled isothermally at 77°F during the addition. The reaction chemistry is:
Na (liq.) + H2O (liq.) → NaOH (aq.) + ½H2 (gas)
The reaction occurs in a vessel with a 5-ft outer diameter and a ¼-in.-thick shell, equipped with a bottom ASME F&D head. The straight wall holds 144.5 gal/ft of liquid height. The bottom head holds 73.9 gal. The straight side has a wetted area of 15.7 ft2/ft of liquid height. The outside surface area of the bottom head is 23.2 ft2. Table 1 presents a heat and material balance for this reaction.
Let’s now estimate the addition time, assuming an overall heat transfer coefficient of 80 BTU/hr/ft2/°F and 25,000 lb/hr of 41°F chilled water flow (Cp = 1) to the jacket.
Step 1. Calculate the liquid density, ρ.
Per Table 1, the change in volume is 712.0 - 795.9 = -83.9 gal = -11.2 ft3. The change in weight is 2,928.9 + 5,276.9 - 6,610.3 = 1,595.5 lb. The liquid density for this reaction is 1,595.5 lb/(-11.2 ft3) = -142.5 lb/ft3. (Surprise! The density is a negative number because the total volume shrinks after the addition.)
Step 2. Calculate the heat of reaction.
Per Table 1, the heat liberated is the sum of the product enthalpies minus the sum of the reactant enthalpies, i.e., [0.0 + (-82.0) + (-14,540.7) + (-36,050.0)] - [179.0 + (-45,159.4)] = -5,692.3 kBTU. The net weight added to the reactor is 1,595.5 lb. (Surprise! It doesn’t equal the weight of the sodium metal because of the evolution of hydrogen gas.) The heat of reaction is then -5,692.3 kBTU/1,595.5 lb = -3.568 kBTU/lb or -3,568 BTU/lb.
