Properly Assess Economics
Many engineering choices depend upon economics. You must select the path forward that will earn the most (or lose the least). The three most common methods for evaluating economic value of projects are simple payback, net present value (NPV) and internal rate of return (IRR). Each offers a different type of answer. Simple payback details a duration. NPV gives a total value. IRR yields a percent or fraction. All three have specific situations where they might be the right approach.
[pullquote]
Let’s focus here on when to use NPV versus IRR. Both use a time-discount factor. It recognizes that money in-hand today is worth more than money in the future. Both NPV and IRR consider cost of funds (COF), which is an externally imposed cost of using capital.
Capital can come from different sources. If the funds are from a loan, COF includes the interest rate on the loan plus the loan’s administrative and overhead costs. If the money is from equity, COF represents the return required to tempt investors to buy shares in a firm.
NPV is defined as the expected total value of a project above the cost of funds required to finance the project. The simplest definition of IRR is that it is the cost of funds that brings the NPV down to zero.
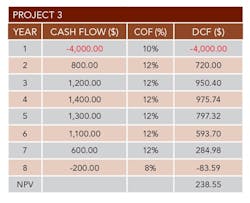
Table 1 illustrates simplified examples of three projects. All three use a basis that all funds are expended or received at the start of the year. Table 1 includes the year, cash flow, COF, discounted cash flow (DCF) and total NPV.
• Project 1 has a high NPV and a low IRR.
• Project 2 has a low NPV and high IRR.
• Project 3 is shown with only an NPV.
This looks confusing? Which would be the better project to invest in?
NPV concentrates on total wealth creation. A higher NPV gives a higher total wealth gain. In general, use NPV when:
• The projects are exclusive. You can do either Project 1 or Project 2 but not both.
• The projects have complex cash flow patterns. Project 3 is a good example.
• The projects have different expected productive lives. Again, Project 3 is a good example.
• The projects have variable expected COF values, as in Project 3.
IRR concentrates on investment efficiency. In general, use IRR when:
• The projects are additive. You can invest in both Project 1 and Project 2 if you want.
• The projects have smooth cost flow patterns.
NPV tends to be more flexible. NPV can handle nearly any combination of project life, cash flow quantity and direction, and allows for variable COF over time. NPV nearly always is the right choice when projects are exclusive. An example is building a plant in Location A (Project 1) versus Location B (Project 2) to supply a fixed market. You only will build one plant. Once a choice is made, the other option is eliminated. Many other cases exist, including situations with limited supply of feed or physical space constraints inside an existing plant. NPV investment decisions tend to favor large projects over smaller ones because large cash flows can give larger NPV totals.
IRR tends to be simpler to understand. Many people prefer to think in percentages rather than in quantities. The examples in Table 1 use numerical methods to get the NPV and IRR values. IRR assumes you have a free choice of projects. A nearly perfect example of using an IRR calculation is investment in the stock market. You can invest in many stocks. Investing in one stock does not shut off the option of investing in additional stocks as well. IRR investment decisions tend to favor smaller projects that have relatively high returns.
Table 1. Project 1 offers a higher net present value (NPV) but Project 2 provides a higher internal rate of return (IRR).
Simplified methods to calculate NPV and IRR are available. Such simplified methods often assume a fixed outflow amount followed by a constant inflow of funds for a fixed period of time. These simplified methods may give nonsense answers for complicated cash flows. Additionally, some IRR formulas assume cash generated by a project will be reinvested at the IRR. Others assume net cash generated will be reinvested at a different COF rate. With complicated cash flows, even the meaning of IRR becomes ambiguous. For this reason, no IRR was included for Project 3.
A single project decision may use both NPV and IRR. Projects may be partly exclusive. Both total wealth and investment efficiency may be important. NPV and IRR also may be combined for project optimization. You might use NPV to make a preliminary decision between projects and then rely on IRR to optimize specific investments within a larger project. An example of this is using NPV to determine plant location and then using IRR to determine the value of energy efficiency on the final plant.
Other factors, such as comparing projects at constant feed rate versus a constant product rate, also may require combinations of different methods (see: “Correctly Evaluate Project Economics.”)
When deciding between NPV and IRR, remember:
• Both use a discount for the time value of funds.
• NPV focuses on total return. Use when projects are exclusive.
• IRR focuses on investment efficiency. Use when projects can overlap.