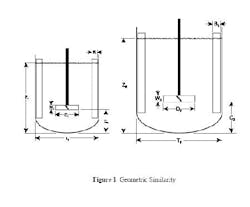
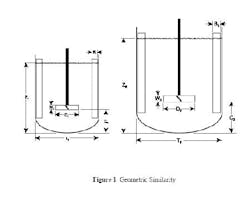
A production mixing unit is usually not geometrically similar to the mixer used for process development. Such differences can make scale-up from the laboratory or pilot plant challenging. A solution to these problems is to systematically calculate and evaluate mixing characteristics for each geometry change.
Geometric similarity is often used in mixing scale-up because it greatly simplifies design calculations. Geometric similarity means that a single ratio between small scale and large scale applies to every length dimension (see figure). With geometric similarity, all of the length dimensions in the large-scale equipment are set by the corresponding dimensions in the small-scale equipment. The only remaining variable for scale-up to large-scale mixing is the rotational speed — one or more mixing characteristics, such as tip speed, can be duplicated by the appropriate selection of a large-scale mixer speed.
The two most popular and effective geometric scale-up methods are equal tip speed and equal power per volume. Equal tip speed results when the small-scale mixer speed is multiplied by the inverse geometric ratio of the impeller diameters to get the large-scale mixer speed:
N2 = N1(D1/D2)
Equal power per volume involves a similar calculation, except the geometry ratio is raised to the two-thirds power:
N2 = N1(D1/D2)(2/3)
This expression for power per volume only applies strictly for turbulent conditions, where the power number is constant, but is approximately correct for transition-flow mixing.
Another important mixing characteristic is torque per volume, which often represents mixing intensity, in terms of fluid velocities. While torque is just power divided by speed, torque per volume is similar to momentum transfer and is closely related to the effective motion created by the mixer. For geometric similarity and turbulent conditions, torque per volume reduces to the same scale-up formula as equal tip speed (Eq. 1). Most of the practical scale-up rules for geometric similarity, including equal solids suspension, fall in the speed range between equal tip speed and equal power per volume. Other criteria, such as equal blend time or surface motion are difficult to scale-up because of the rapidly increasing mixing intensity for large-scale tanks.
The sidebar gives formulas for calculating mixing variables in conventional U.S. engineering units. Derivations and details on the various equations for geometric scale-up and mixer evaluation appear in many references such as widely available handbooks [Refs. 1 and 2].
Five steps
The recommended approach for doing non-geometric scale-up is as follows:
1. Calculate the laboratory- or pilot-plant-scale values for the mixing variables listed in the sidebar.
2. Do a geometric-similarity scale-up to the large-scale tank diameter. Use a criterion such as tip speed to set the large-scale speed. Calculate the mixing variables for the new, large-scale conditions.
3. As needed, change the impeller diameter at the large scale. Calculate the mixing variables and, if required, modify speed to keep an important variable such as tip speed or torque per volume constant.
4. Switch impeller type, if desired or necessary, and recalculate mixing variables using the appropriate power number for the new impeller. Calculate the mixing variables and make decisions or adjustments as required.
5. Alter the liquid level, if necessary, to match volume specifications at the large scale. Calculate the mixing variables again for the new liquid level. If undesirable changes occur, adjust mixer speed or number of impellers.
The key to success is making simple step-by-step changes in the design and calculating important variables each time. In this way, you can evaluate the cause and effects of changes and make corrections when necessary.
Applying the approach
Suppose for example, we did a series of experiments with a 5.0 gal. batch in an 11.5 in.-dia. pilot reactor, which had two 5-in.-diameter, three-blade, pitched-blade turbines, and found that we could get good results with the mixer operating at 300 rpm. The material we were mixing had a final viscosity of 85 cP and a specific gravity of 1.05. Rearranging the volume formula in the sidebar and plugging in values, we can find the liquid level for 5.0 gal. in a 11.5 in.-diameter cylindrical tank:
H = 4 (231)(5)/p(11.5)2 = 11.12 in.
The 11.12-in. liquid level assumes that the tank bottom is flat and the tank internals (impellers, shaft, baffles, etc.) do not take up any space. In the real world, the tank may have a dished bottom and the internals typically will occupy 2% to 5% of the volume for this type of reactor. While corrections can be made for bottom shape and tank internals, for simplicity we will ignore these corrections here.
With this information, we can calculate the operating conditions that exist in our pilot-scale experiment (see table). At these conditions, the Reynolds number of 995 would suggest that the mixer is operating in the transition regime, which applies for 1 < NRe < 20,000. For a pitched-blade turbine the power number, which remains constant in the turbulent range, will begin to increase in the transition and viscous regime. For simplicity, let’s assume that the power number does not begin to increase until the Reynolds number drops below 900. Had the Reynolds number been less than 900, we would have to make an appropriate correction to the power number and use that corrected number to calculate power and torque characteristics of the mixer. This additional step to correct power number should be done for each subsequent step in the scale-up process if the Reynolds number suggests that such a correction is necessary. (Power number corrections differ with type of impeller.)
Now suppose we want to duplicate our process results in an 84.0 in.-dia. tank with a 3,000 gal capacity using four-blade, pitched-blade turbines. As we will see while doing the calculations, the tank geometry and impeller type both change in the scale-up process. Such changes are common. In this particular case, a combination of experience, literature research and experimentation leads us to believe that the tip speed should be held constant when we scale-up and that torque-per-volume may represent mixing intensity.
As a first step in our scale-up calculation, we will use geometrical similarity to do a scale-up from our 11.5 in.-dia. pilot tank to an 84-in.-dia. process tank. Geometric similarity means that our scale-up length ratio of 84/11.5 = 7.3 will multiply all of the length dimensions. Thus, the 5.0 in.-dia. pilot turbine will scale-up to a 36.5 in.-dia turbine in the large-scale tank and the liquid level will be 7.3 × 11.12 = 81.2 inches. However, this liquid level provides a volume of only 1,948 gal. We will need to adjust the liquid level later to get our desired results.
To maintain the same tip speed in the large-scale mixer as in the pilot unit, we must adjust rotational speed because the impeller diameters differ and impeller diameter times rotational speed gives tip speed. So, for equal tip speed, the operating speed for the large-scale mixer is:
300 (11.5/84) = 41.1 rpm
At 41.1 rpm, we can do the same calculations we did for the pilot-scale results.
As shown in the table, geometric scale-up with constant tip speed increased the Reynolds number, power and torque. However, power per volume decreased and torque per volume remained constant. For this first step in our scale-up process, both tip speed and torque per volume remained constant, which satisfies our process scale-up objectives.
The next step
At this point we will change to the four-blade turbines required in our large-scale process. The four-blade turbines have a power number of 1.37 instead of 1.19; so we can round down the turbine diameter to 36.0 in. and round up the speed to 42.0 rpm. Such adjustments seem both reasonable and practical. However, we should recalculate our mixing results to be sure.
With this turbine change, tip speed essentially stays constant and our torque per volume rises by a little more than 20%. This increased torque per volume represents a possible boost in apparent mixing intensity, which could be judged to be beneficial, because the larger tank will blend more slowly than the small pilot tank.
Adjust the tank volume
Now we need to increase tank volume to the required 3,000 gal. for the full-scale process. We can achieve this by raising the liquid level to 125 in. from the geometric value of 81.2 in. We must check the effects of the larger volume on the mixing variables.
Because the volume changed but not the mixer, only the power per volume and torque per volume changed. The torque per volume is now only 80% of our original pilot and geometric-scale-up values, which might translate into too little mixing and thus uneven results.
Several possible remedies exist for the undesired reduction in torque per volume. Suppose that with the volume increase we had held both the tip speed and torque per volume constant. For such a scenario, both the turbine diameter, D, and rotational speed, N, must change as the volume increases. To keep tip speed constant, we can use the relationship:
vTIP ∝ND
Then, per Eq. 1, for constant tip speed:
N2D2 = N1D1
For torque per volume, the following relationship based on turbulent conditions applies:
t/V ∝ N2D5/V
For constant torque per volume:
N22D25/V2 = N12D15/V1
Factoring tip speed out of the constant torque per volume relationship gives:
(N22 D22) D23/V2 = (N12 D12) D13/V1
which for constant tip speed can be reduced to:
D23/V2 = D13/V1
Rearranging Eq. 7 and solving for the new turbine diameter gives:
D2 = D1(V2/V1)1/3 = 36(3000/1948)1/3 = 41.6 in.
Using the new turbine diameter, a speed can be selected to satisfy the constant tip-speed condition:
N2 = N1(D1/D2) = 42 (36.0/41.6) = 36.3 rpm
According to the algebra, this larger turbine and lower speed should keep both tip speed and torque per volume constant; this can be checked by recalculating mixing values.
By similar methods other combinations of variables, such as tip speed and power per volume, could be held constant. Also, impeller type can be changed and mixing variables held constant by including the power number in the expressions for power or torque. Many different adjustments to mixer characteristics can be handled by similar expressions and manipulations. Usually only a couple of mixing variables can be held constant while the others change. Sometimes this will lead to impractical solutions such as extreme impeller diameters or rotational speeds. If viscosity, through Reynolds number, affects power number, the exact mathematical relationships do not hold for power and torque. In those cases estimate approximate values and adjust calculated mixing values if necessary.
Returning for a moment to the volume change that was necessary in going from the geometrically similar scale-up to the actual large-scale volume, another possibility should be considered. The geometric scale-up resulted in a volume of 1,948 gal., yet the large-scale process required 3,000 gal. The ratio of the volumes is almost exactly 2:3, so why not consider going from two turbines to three turbines. The resulting changes in the calculated values are shown in the table. This solution to the scale-up problem not only meets the large-scale process requirements but also maintains the desired characteristics of the pilot-plant situation.
Avoid mix-ups
As we have seen, taking successive steps allows the development of alternative solutions to scale-up. Similar methods can be used to scale-down process problems for investigation in a pilot-plant or laboratory simulation. Here, too, non-geometric similarity often is a problem. Such scale-down calculations should help pinpoint appropriate operating speeds to test in the small-scale mixer.
In any scale-up or scale-down evaluation, some variables can be held constant while others must change. For example, even with geometric similarity, scale-up will result in less surface per volume because surface area increases as the length squared and volume increases as length cubed. Similarly, keeping blend time constant rarely is practical with any significant scale change. Larger tanks take longer to blend than smaller ones. Also, Reynolds number is expected to increase as size increases. In addition, standard operating speeds or available impeller sizes may necessitate a final adjustment to the scale-up calculations.
Rules for scale-up always have exceptions but understanding the effects of scale-up, especially non-geometric scale-up, can provide valuable guidance. Indeed, appreciation of the tradeoffs involved in non-geometric scale-up may be crucial for success with large-scale mixing processes.
Dr. David S. Dickey is senior consultant at MixTech, Inc., Dayton, Ohio. He teaches a short course on pilot-plant scale-up methods for industrial mixing for the University of Wisconsin. E-mail him at [email protected].
REFERENCES
1. “Perry’s Chemical Engineers’ Handbook,” 7th ed., Green, D.W. and J.O. Maloney, Eds., McGraw-Hill, New York (1997).
2. “Handbook of Industrial Mixing, Science & Practice,” Paul, E.L., et al., Eds., Wiley, Hoboken, N.J. (2004).
NOMENCLATURE
D = impeller diameter, in.
H = liquid level, in.
N = rotational speed, rpm
P = power, hp
T = tank diameter, in.
V = volume, gal
v = velocity, ft/min
= viscosity, cP
ρ = specific gravity
KEY EQUATIONS
Impeller power, hp P = NPρN3D5/(1.524 × 1013)
Power per volume, hp/1,000 gal PV = 1,000 P/V
Power number NP = (1.524 × 1013)P/r N3 D5
Reynolds number NRe = 10.74 D2Nρ/m
Tank volume, cylindrical tank, gal V = (π/4)(T2H/231)
Tip speed, ft/min vTIP = πDN/12
Torque, in.-lb t = 63,025 P/N
Torque/volume, in.-lb/1,000 gal tV = 1,000 t/V