Keep metering problems from bubbling up

Coriolis meters have long been used very successfully on single-phase fluids. However, liquids that contain bubbles (air or gas) cause dynamic changes to a Coriolis meter that are not present in a single-phase fluid and that lead to measurement errors.

A Coriolis meter operates by driving one or two tubes at a resonant, or natural, frequency. In the meter, the electronics (or transmitter) send a drive signal to the sensor that tracks the frequency of the tube and maintains the proper vibration amplitude. Driving on the resonant frequency is important because it enables fluid density measurement and minimizes power requirements.

All modern Coriolis meters are intrinsically safe (IS), which limits the amount of power that is allowed to drive the sensor. Bubbles moving around in the liquid tremendously increase fluid damping, which results in power requirements that far exceed what IS restrictions permit. So, the tube amplitude significantly decreases. This condition is sometimes called stall, although the tubes usually do continue to vibrate to some extent.

[javascriptSnippet ]

When the tube amplitude decreases, the signal-to-noise ratio also falls, making it a challenge to extract the mass flow signal from the relatively high level of noise. Older analog signal-processing techniques are highly sensitive to entrained air because signal amplitude is low and noise is high; no algorithm is available to enhance the measurement signal, thereby improving the signal-to-noise ratio. In contrast, digital signal processing (DSP) can effectively filter the noise to yield a good stable measurement so long as the tube is vibrating, even at reduced amplitudes.

Note: Even with DSP, when gas is present in a liquid stream the meter can only provide total-product density (including the gas), not liquid-only density.

The impact of fluid dynamics
Coriolis meters are not sensitive to flow profile and other disturbances that affect other metering technologies. For instance, since the fundamental measurement of delta T comes from the relative values of each of two tubes in bent-tube designs, swirl upstream of the meter doesnt impact the measurement because it doesnt matter how much flow goes through one tube or the other. Accuracy is not degraded even when one tube is completely plugged.

However, when gas is present in a liquid, the flow profile can become a concern. Although the fundamental measurement is unaffected (that is, the relative delta T), the tubes can become imbalanced due to the large density difference between them (air in one, liquid in the other, for instance). An imbalance can cause meter zero errors; therefore, measuring low flow rates can be problematic.

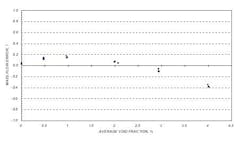
An equally significant problem occurs at rates too low to sweep bubbles out of the tubes. If the fluid velocity is less than approximately 0.6 m/s, air will hang up in tube regions where the flow is against gravity (Figure 1). Bubbles get caught in the inlet tube leg because fluid velocity is not great enough to push the bubbles down and out against gravity forcing the bubbles up. This issue is present in any bent-tube meter design because at some location in the tube the fluid velocity is fighting gravity.

Figure 1

When fluid velocity cant overcome buoyancy, bubbles get caught in inlet leg.

The solution is to keep flow rate high enough such that fluid velocity can purge the sensor of air. A rate of 20% of meter nominal flow (1 m/s in the flow tube) or higher is adequate to completely purge the meter of bubbles and give good performance. In a U-shaped meter, mounting the sensor in a vertical pipe run with flow going up helps to keep the bubbles moving through the meter.

The role of fluid properties
Pressure, fluid temperature and viscosity all impact how a Coriolis meter deals with varying levels of entrained air.

As pressure increases or decreases, the apparent void fraction changes, of course. This means, for instance, if two meters are piped in series, the downstream meter is at a distinct disadvantage because the pressure is lower and therefore the void fraction is higher.

Temperature plays a minor role, in that it affects viscosity and surface tension. It also impacts void fraction to a small degree (higher temperature results in higher void fraction).

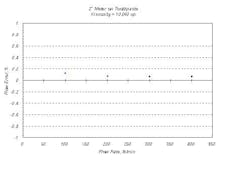
Viscosity is a very important fluid parameter because it directly influences the propensity of the fluid to hold up air (or gas). In a low-viscosity liquid such as water, air bubbles coalesce from finely distributed small bubbles into large ones that collect at high points in the line. In contrast, if the bubbles stay finely distributed, as happens in high-viscosity liquids, they will be purged from the meter easily and not collect and metering will be accurate. Figure 2 shows results for toothpaste with a viscosity of 10,000 cP and entrained air level between 2 and 5%. Rates are quite low for a 2-in. meter (<0.6 m/s) yet performance is well within specification.

Figure 2

Even at low flow rate, measurements for 10,000-cP toothpaste with 2-5% void fraction are within specification.

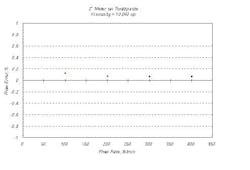
The opposite viscosity extreme is water where air will always tend to separate. If velocity is high, bubbles tend to stay finely divided, which helps to keep the air well mixed. Figure 3 shows very good performance because mixing is good due to the high flow rate (38,000 kg/h). If the velocity is low, bubbles collect at locations in the meter flow tubes or piping where the flow direction is against gravity. Errors can easily exceed 5% if the velocity is less than 0.6 m/s and therefore mixing is poor.

Figure 2

Meter provides accurate results for water containing up to 4% void fraction because flow rate is high, 38,000 kg/h.

Future improvements
Transmitters in development will enable accurate measurement of lower rates. There will always be a physical limit to the minimum rate that can be measured because of the previously described separation issues. However, noise rejection improvement with new DSP techniques will allow the minimum rate to be pushed lower.

A significant problem with any two-phase flow (water/air, dog food with solids suspended in water, oil/gas, etc.) is at zero flow. When the flow is stopped, the multiple phases separate by gravity, prompting an imbalance in the tube. This imbalance causes an apparent meter zero change. Work on signal processing improvements to address this problem is currently a significant area of research.

Tim Patten is director of measurement technology for Micro Motion, Inc., Boulder, Colo. E-mail him at [email protected].

A special case
Empty-full-empty batching can pose a related measurement issue. Such batching is most common to avoid cross-contamination of products when filling large tanks such as rail cars or trucks. Therefore, the loading line is purged with air or other inert gas between loads, leaving the meter empty before and after the batch.

Generally, this application is not too difficult because the batches tend to be long (greater than one minute). Any transient meter behavior at the beginning and end of the batch is small compared to the whole batch, so errors are washed out.

However, when batches are short (less than one minute), the transient errors can account for a significant fraction of the total error. Air may be entrained for a brief period, but the main issue is the time it takes to fill the meter with fluid. For instance, an application running at 3 m/s will take about 0.1 s to fill if the tube length is 0.3 m; an application at 0.3 m/s will take a full second simply to fill the meter. Experience has shown that if the meter fill-time is less than 0.1 sec., good batching performance can be achieved, regardless of the meters tube geometry.